What is an "Anti-Ackermann" steering geometry? And why is it so used in Formula 1?

We all know how important it is for a Formula 1 single-seater to extract the maximum performance out of the tyres: even if it may seem like a clichè, it's still true that the tyres are the only contact patch between the car and the ground.

This means that all the forces generated during a lap - or an entire race - can only be transferred to the ground via the tyres. If we think about it, what's the point of designing a car capable of generating huge values of downforce if this doesn't give it more grip in the cornering phase? Obviously very little, when the ultimate goal is to set competitive laptimes...

Among the components that must be put at the service of tyre performance we certainly have to mention the steering mechanism (and its geometries), designed according to a criterion often called "Anti-Ackermann". But let's start from the beginning...

Ackermann Steering geometry

Suppose we observe a vehicle from above as it travels a left corner with a constant radius R. For the sake of thoroughness, the reference image shows the geometric data relating to the track "a" and the wheelbase of the vehicle "l".

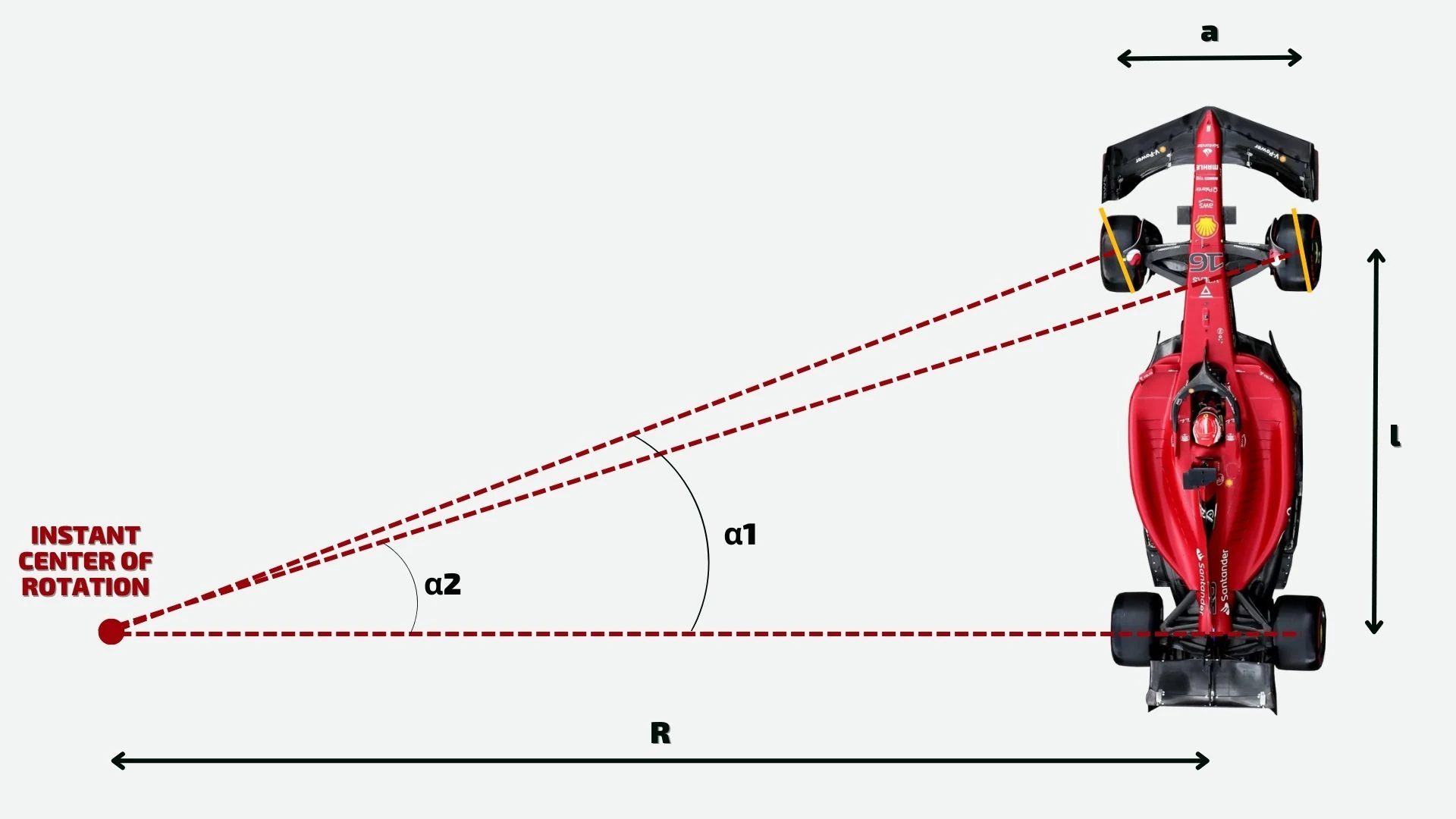
Geometric scheme of a vehicle during a left corner

In such a scenario, obviously considering the rear wheels as non-steering, the theory implies that in order to reduce tyre sliding, the steering angle must be greater for the front right wheel than for the front left. Obviously, if the corner analyzed were a right one, the situation would reverse in a perfectly specular way; but, keeping it simple, let's continue to consider the case of a left turn.

The difference between the steering angle of each of the two front wheels, however, is not accidental: in order to (virtually) eliminate tyre sliding, let's consider the geometric construction sketched above. There, we observe how the axes starting from the two wheel centers intersect at a point also belonging to the rear axle... this point is called the "instant center of rotation", and neglecting all the secondary effects that act during the motion of a vehicle (again for simplification purposes), we want to ensure that it remains fixed over time.

What we've just described is called kinematic steering condition, or also "Ackermann's condition". Mathematically, this scenario is fully realized if the two angles α1 and α2 satisfy the following formulae:

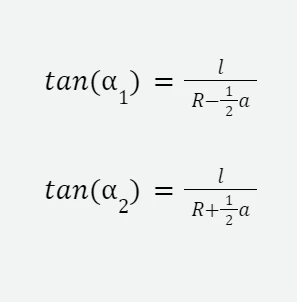
The kinematic steering condition is so important that it's taken as a reference to define the "Ackermann percentage", a parameter that gives us a measure of how close a steering mechanism is to the ideal scenario just discussed. To give you an idea, we have:

• An Ackermann percentage of 100% if the kinematic steering condition is perfectly replicated;
• An Ackermann percentage of 0% if the two steering wheels have the same steering angle;

What implications do the considerations made on a moving vehicle have?

All that we have expressed in the previous paragraph means that, whatever the Ackermann percentage, visually we would (correctly) perceive the outside wheel as being steered with a smaller angle compared to the inside one... the only thing that changes is that this effect intensifies as we go from a value of 0% to one of 100%.

But in Formula 1, as we are about to find out, things are absolutely not like this...

Formula 1 steering: an Anti-Ackermann geometry is preferred

To understand what results the technical development of the steering geometries has led to, just look at the following image, where Pierre Gasly approaches the apex of a right-hand corner with his Alpine A523.

Front wheels steering during a right-hand corner (Pierre Gasly, Alpine A523) - Credit: F1TV

As can be seen thanks to the green dotted lines, the two front wheels appear - and are - converging: the outer wheel, in this case the left, is steering much more than the inner one (the right wheel)... This is in perfect antithesis with what was explained up to a few lines ago. How come?

What we observe is an "Anti-Ackermann" geometry, where in order to increase the lateral grip a large amount of relative sliding between tyres and asphalt is accepted, and with it the consequent tyre wear. The friction generated due to this sliding is so high that it has the effect of reducing the vehicle speed almost as if the driver were pressing the brakes... certainly a useful technique when there's the risk of missing the apex, although it goes without saying that relying on this phenomenon takes the driver's sensitivity away...

How to find the optimal "Slip Angle" to improve grip?

At this point, we understand that the direction in which the steering wheels are pointing is fundamental for the level of grip with which a driver can approach a corner: let's try to introduce an element of complication for a moment, introducing in our model the phenomenon for which the inertial forces tend to deform the tyre construction in an "attempt" to push the vehicle towards the outside of the corner.

In fact, the inertial forces cause a certain amount of lateral slip, so an angle can be defined between the direction in which the wheels "point" and the one in which the vehicle actually travels: we are talking about the so-called "slip angle". The question that the engineers are asking themselves then becomes: what slip angle corresponds to the maximum lateral grip obtainable?

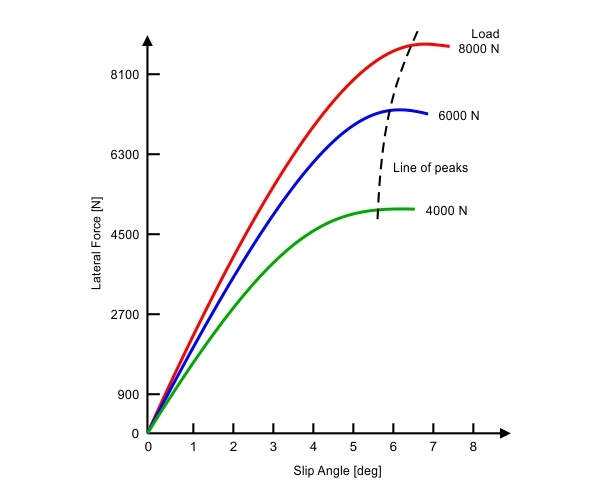
Lateral Grip versus Slip Angle of a tyre - Credit: Rodrigo Santos (racingcardynamics.com)

The graph above shows quite clearly (red line) that in order to increase the grip level provided by a racing tyre it's necessary to design steering mechanisms that incorporates a greater than zero slip angle: it's precisely for this reason that Anti-Ackermann steering is used!

Obviously for less extreme racing tyres (blue line) and for road tyres (green line) the situation is much less extreme, and also for this reason - as well as to reduce their wear - road vehicles are designed with steering angles that are far from being Anti-Ackermann ones...

What further complicates the design?

In conclusion, it should be noted that all the content of this article could be analyzed under an even more critical lens, introducing parameters such as the vehicle ride height, its mass, its downforce level and the distinction between a dry track and a wet one.

All these conditions being equal, what has been said remains valid: then you'll certainly understand how the design of a Formula 1 single-seater can never aim to get the most out of any component that makes it up, because often what helps in reaching a target is detrimental to other ones...

Using the steering mechanism as an example, we just learned that using an Ackermann percentage of 100% in F1 would mean enormously reducing tyre wear, which would be excellent... But at the same time it would mean having less grip available (and therefore a slower car on the corners), therefore the proposed solution becomes much less attractive!

Long story short, as mentioned several times, design requirements are pretty much always the result of trade-offs... But if you love the technical aspect of Formula 1, you already knew this!

Hoping you enjoyed this in-depth analysis, I remind you that you can also follow Race Analysis on Instagram, Twitter and YouTube. Until next time!